Types of Gears

There are many types of gears such as spur gears, helical gears, bevel gears, worm gears, gear rack, etc. These can be broadly classified by looking at the positions of axes such as parallel shafts, intersecting shafts and non-intersecting shafts.
It is necessary to accurately understand the differences among gear types to accomplish necessary force transmission in mechanical designs. Even after choosing the general type, it is important to consider factors such as: dimensions (module, number of teeth, helix angle, face width, etc.), standard of precision grade (ISO, AGMA, DIN), need for teeth grinding and/or heat treating, allowable torque and efficiency, etc.

Besides this page, we present more thorough gear technical information under Gear Knowledge (separate PDF page). In addition to the list below, each section such as worm gear, rack and pinion, bevel gear, etc. has its own additional explanation regarding the respective gear type. If it is difficult to view PDF, please consult these sections.
It is best to start with the general knowledge of the types of gears as shown below. But in addition to these, there are other types such as face gear, herringbone gear (double helical gear), crown gear, hypoid gear, etc.
Short movie "Easy Gear Selection"
Applications of Gears in Various Industries
Robotics
Humanoid Robots
Semiconductor Equipment
Medical Device
Machine Tools
Industrial Automation
Food Processing Equipment
-
Spur Gear
Gears having cylindrical pitch surfaces are called cylindrical gears. Spur gears belong to the parallel shaft gear group and are cylindrical gears with a tooth line which is straight and parallel to the shaft. Spur gears are the most widely used gears that can achieve high accuracy with relatively easy production processes. They have the characteristic of having no load in the axial direction (thrust load). The larger of the meshing pair is called the gear and smaller is called the pinion.
Click Here to Select Spur Gears
KHK's Anti-backlash Gears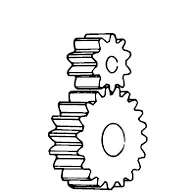
A sketch of spur gears
-
Helical Gear
Helical gears are used with parallel shafts similar to spur gears and are cylindrical gears with winding tooth lines. They have better teeth meshing than spur gears and have superior quietness and can transmit higher loads, making them suitable for high speed applications. When using helical gears, they create thrust force in the axial direction, necessitating the use of thrust bearings. Helical gears come with right hand and left hand twist requiring opposite hand gears for a meshing pair.
Click Here to Select Helical Gears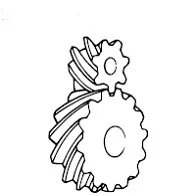
A sketch of helical gears
-
Gear Rack
Same sized and shaped teeth cut at equal distances along a flat surface or a straight rod is called a gear rack. A gear rack is a cylindrical gear with the radius of the pitch cylinder being infinite. By meshing with a cylindrical gear pinion, it converts rotational motion into linear motion. Gear racks can be broadly divided into straight tooth racks and helical tooth racks, but both have straight tooth lines. By machining the ends of gear racks, it is possible to connect gear racks end to end.
Click Here to Select Gear Rack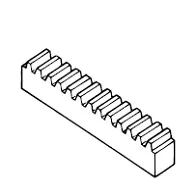
A sketch of gear rack
-
Bevel Gear
Bevel gears have a cone shaped appearance and are used to transmit force between two shafts which intersect at one point (intersecting shafts). A bevel gear has a cone as its pitch surface and its teeth are cut along the cone. Kinds of bevel gears include straight bevel gears, helical bevel gears, spiral bevel gears, miter gears, angular bevel gears, crown gears, zerol bevel gears and hypoid gears.
Click Here to Select Bevel Gears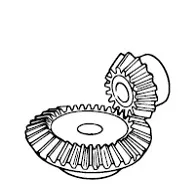
A sketch of bevel gears
-
Spiral Bevel Gear
Spiral bevel gears are bevel gears with curved tooth lines. Due to higher tooth contact ratio, they are superior to straight bevel gears in efficiency, strength, vibration and noise. On the other hand, they are more difficult to produce. Also, because the teeth are curved, they cause thrust forces in the axial direction. Within the spiral bevel gears, the one with the zero twisting angle is called zerol bevel gear.
Click Here to Select Spiral Bevel Gears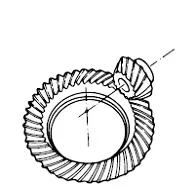
A sketch of spiral bevel gears
-
Screw Gear
Screw gears are a pair of same hand helical gears with the twist angle of 45° on non-parallel, non-intersecting shafts. Because the tooth contact is a point, their load carrying capacity is low and they are not suitable for large power transmission. Since power is transmitted by the sliding of the tooth surfaces, it is necessary to pay attention to lubrication when using screw gears. There are no restrictions as far as the combinations of number of teeth.
Click Here to Select Screw Gears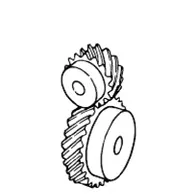
A sketch of screw gears
-
Miter Gear
Miter gears are bevel gears with a speed ratio of 1. They are used to change the direction of power transmission without changing speed. There are straight miter and spiral miter gears. When using the spiral miter gears it becomes necessary to consider using thrust bearings since they produce thrust force in the axial direction. Besides the usual miter gears with 90° shaft angles, miter gears with any other shaft angles are called angular miter gears.
Click Here to Select Miter Gears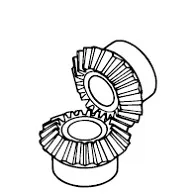
A sketch of miter gears
-
Worm Gear
A screw shape cut on a shaft is the worm, the mating gear is the worm wheel, and together on non-intersecting shafts is called a worm gear. Worms and worm wheels are not limited to cylindrical shapes. There is the hour-glass type which can increase the contact ratio, but production becomes more difficult. Due to the sliding contact of the gear surfaces, it is necessary to reduce friction. For this reason, generally a hard material is used for the worm, and a soft material is used for worm wheel. Even though the efficiency is low due to the sliding contact, the rotation is smooth and quiet. When the lead angle of the worm is small, it creates a self-locking feature.
Click Here to Select Worm Gears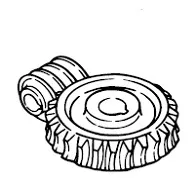
A sketch of worm gears
-
Internal gear
Internal gears have teeth cut on the inside of cylinders or cones and are paired with external gears. The main use of internal gears are for planetary gear drives and gear type shaft couplings. There are limitations in the number of teeth differences between internal and external gears due to involute interference, trochoid interference and trimming problems. The rotational directions of the internal and external gears in mesh are the same while they are opposite when two external gears are in mesh.
Click Here to Select Internal Gears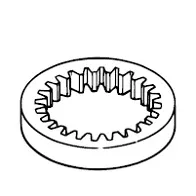
A sketch of internal gear
What is a gear ?
A gear is a kind of machine element in which teeth are cut around cylindrical or cone shaped surfaces with equal spacing. By meshing a pair of these elements, they are used to transmit rotations and forces from the driving shaft to the driven shaft. Gears can be classified by shape as involute, cycloidal and trochoidal gears. Also, they can be classified by shaft positions as parallel shaft gears, intersecting shaft gears, and non-parallel and non-intersecting shaft gears. The history of gears is old and the use of gears already appears in ancient Greece in B.C. in the writing of Archimedes.

A sample box of various types of gears
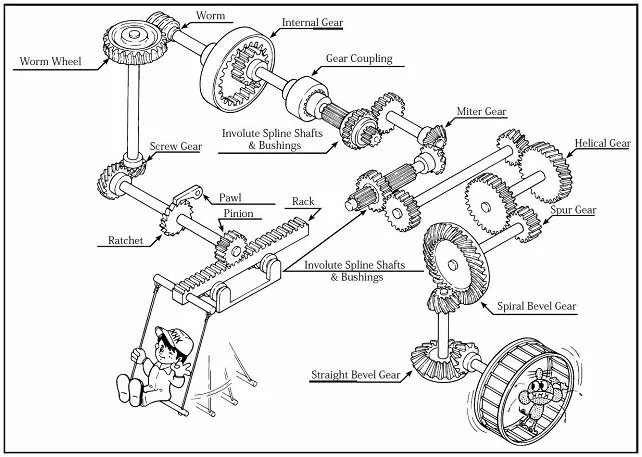
An overview of gears
(Important Gear Terminology and Gear Nomenclature in this picture)
- Worm
- Worm wheel
- Internal gear
- Gear coupling
- Screw gear
- Involute spline shafts and bushings
- Miter gear
- Spur gear
- Helical gear
- Ratchet
- Pawl
- Rack
- Pinion
- Straight bevel gear
- Spiral bevel gear
There are three major categories of gears in accordance with the orientation of their axes
Configuration :
- Parallel Axes / Spur Gear, Helical Gear, Gear Rack, Internal Gear
- Intersecting Axes / Miter Gear, Straight Bevel Gear, Spiral Bevel Gear
- Nonparallel, Nonintersecting Axes / Screw Gear, Worm, Worm Gear (Worm Wheel)
- Others / Involute Spline Shaft and Bushing, Gear Coupling, Pawl and Ratchet
The difference between a gear and a sprocket
Simply said, a gear meshes with another gear while a sprocket meshes with a chain and is not a gear. Aside from a sprocket, an item that looks somewhat like a gear is a ratchet, but its motiion is limited to one direction.
Classification of types of gears from the point of positional relations of the attached shafts
- When the gears’ two shafts are parallel (parallel shafts)
Spur gear, rack, internal gear and helical gear, etc.
Generally they have a high transmission efficiency. - When the gears’ two shafts intersect each other (intersecting shafts)
Bevel gear is in this category.
Generally they have a high transmission efficiency. - When the gears’ two shafts are not parallel or intersect (offset shafts)
Worm gear and screw gear belong in this group.
Because of the sliding contact, the transmission efficiency is relatively low.
Precision class of gears
When a type of gears is grouped by accuracy, precision class is used. The precision class is specified by the standards set by ISO, DIN, JIS, AGMA, etc. For example, JIS specifies each precision class’ pitch error, tooth profile error, helix deviation, runout error, etc.
Existence of teeth grinding
Existence of teeth grinding greatly affects the performance of gears. Therefore, in considering types of gears, teeth grinding is an important elememt to consider. Grinding the teeth surface makes gears quieter, increases force transmission capacity and affects the precision class. On the other hand, the addition of teeth grinding process increases cost and is not suitable for all gears. To obtain high precision other than by grinding, there is a process called shaving using shaving cutters.
Kinds of tooth shape
To broadly classify types of gears by their tooth shape, there are involute tooth shape, cycloid tooth shape and trochoid tooth shape. Among these, involute tooth shape is most commonly used. They are easy to produce and has the characteristic of being able to correctly mesh even when the center distance is slightly off. Cycloid tooth shape is mostly used in clocks and trochoid tooth shape is mainly in pumps.
Creation of Gears
This article is reproduced with the permission.
Masao Kubota, Haguruma Nyumon, Tokyo : Ohmsha, Ltd., 1963.
Gears are wheels with teeth and are sometimes called toothed wheels.
Gears are mechanical components that transmit rotation and power from one shaft to another, if each shaft possesses appropriately shaped projections (teeth) equally spaced around its circumference such that as it rotates, the successive tooth goes into the space between the teeth of the other shaft. Thus, it is a machine component in which the rotary power is transmitted by the prime mover’s tooth surface pushing the tooth surface of the driven shaft. As an extreme case, when one side is a linear motion (this can be thought as rotational motion around an infinite point), it is called a rack.
There are many ways to transmit rotation and power from one shaft to another such as by rolling friction, wrapping transmission, etc. However, in spite of a simple structure and a relatively small size, gears have many advantages such as certainty of transmission, accurate angular speed ratio, long lasting and minimal loss of power.
From small clocks and precision measuring instruments (motion transmission applications) to large gears used in marine transmission systems (power transmission applications), gears are used widely and are ranked as one of the important mechanical components along with screws and bearings.
There are many types of gears. However, the simplest and most commonly used gears are the ones used to transmit specific speed ratio between two parallel shafts at a defined distance. In particular, gears with their teeth parallel to the shafts as shown in Figure 1.1 called spur gears are the most popular.
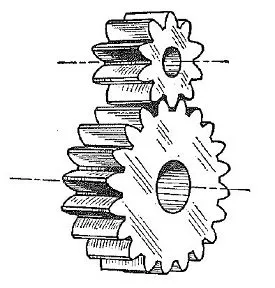
[Figure 1.1 Spur Gears]
The simplest method to transmit specific angular speed ratio between two parallel shafts is a rolling friction drive. This is accomplished as shown in Figure 1.2, by having two cylinders, with diameters in inverse ratio to the speed ratio, in contact and rotating without slippage (if two shafts are counter rotating, contact is on the outside; and if rotating in the same direction, contact is on the inside). That is to say that the rotation is obtained from the friction force of the rolling contact. However, it is impossible to avoid some slippage and, as a result, reliable transmission cannot be hoped for. To get a larger power transmission requires heavier contact forces which in turn result in high bearing loads. For these reasons, this arrangement is not suitable for transmitting large amount of power. As a result, an idea to create suitable form of teeth equally spaced on the rolling surfaces of the cylinders in such a way that at least one pair or more of teeth are always in contact was invented. By pushing the teeth of the trailing shaft with the teeth of the driving shaft, the certainty of a strong transmission is assured. This is called a cylindrical gear and the reference cylinder on which the teeth are carved is the pitch cylinder. Spur gears are one type of cylindrical gears.
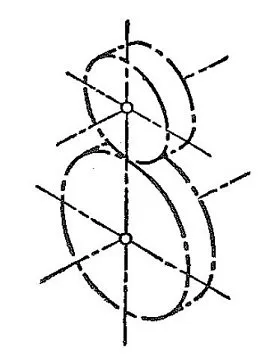
[Figure 1.2 Pitch Cylinders]
When two shafts intersect, the references for carving teeth are the cones in rolling contact. These are the bevel gears as shown in Figure 1.3 where the base cone on which teeth are carved is called the pitch cone. (Figure 1.4).
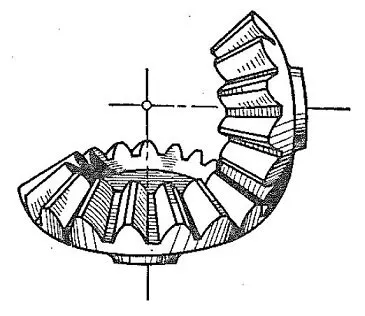
[Figure 1.3 Bevel Gears]
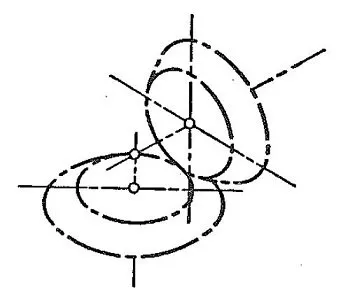
[Figure 1.4 Pitch Cones]
When the two shafts are not parallel and non-intersecting, there are no true rolling contacting curved surfaces. Based on the type of gears, teeth are created on a pair of reference contacting rotating surfaces. In all cases, it is necessary to set the tooth profile such that the relative motion of the contacting pitch surfaces matches the relative motion of the meshing of the teeth on the reference curved surfaces.
When gears are considered as rigid bodies, in order for two bodies to maintain a set angular speed ratio while in contact at teeth surfaces, without running into each other or separating, it is necessary for the common normal components of speed of the of the two gears at the contact point to be equal. In other words, at that instant, there is no relative motion of the gear surfaces in the direction of the common normal, and the relative motion exists only along the contact surface at the point of contact. This relative motion is nothing but the sliding of gear surfaces. The tooth surfaces, with the exception of special points, always involve the so-called sliding contact transmission.
In order for the tooth forms to satisfy the conditions as explained above, utilization of the enveloping surface can lead to the desired tooth form as a general method.
Now, specify one side of gear A’s surface as a curved surface FA, and give both gears a specified relative rotation. Then on the coordinate system attached to gear B, a group of successive positions of the gear surface FA is drawn. Now think of the envelope of this group of curves and use it as the tooth surface FB of gear B. Then from the theory of envelope surfaces, it is clear that the two gear surfaces are in constant line contact and the two gears will have the desired relative motion.
It is also possible to lead to tooth forms by the following method. Consider, in addition to a pair of gears A and B with specified relative motion, a third imaginary gear C in mesh where A and B are in mesh and give it an arbitrary tooth form surface FC (curved surface only without tooth body) and an appropriate relative motion.
Now, using the method as before, from the imagined meshing of gear A with the imaginary gear C, obtain the tooth form FA as the envelope of tooth form FC. Designate the contact line of tooth surfaces FA and FC as IAC. Similarly, obtain the contact line IBC and tooth surface FB from the imaginary meshing of gear B and the imaginary gear C. Thus, the tooth surfaces FA and FB are obtained by the mediation of FC. In this case, if the contact lines IAC and IBC match, gears A and B are in line contact, and if IAC and IBC intersect, gears A and B will have a point contact at that intersection.
That means, with this method, it is possible to lead to point contact tooth forms as well as line contact tooth forms.
However, there are limits to geometrically obtained tooth forms as explained above, especially when the tooth bodies of surfaces FA and FB invade each other, or when those areas cannot be used as tooth forms. This invasion of one tooth body into another is called interference of tooth profiles.
As clear from the above explanation, there are theoretically many ways to produce tooth forms which create specified relative motion. However, in reality, consideration for the gear mesh, tooth form strength and difficulties of tooth cutting will limit the usage of these kinds of tooth forms to just a few.
Free Gear Technical Data available in PDF format
KHK offers for free the “Gear Technical Data” book in PDF format. This book is very useful for learning about gears and gearing. In addition to the types of gears and gear terminology, the book also includes sections regarding tooth profile, calculations of dimensions, strength calculations, materials & heat treatment, ideas about lubrication, noise, etc. You can learn a lot about gearing from this book.
The ways to use gears in mechanical design situations
Gears are primarily used to transmit power, but, based on ideas, they can be utilized as machine elements in different ways. Below are introductions to some of the ways.
- Grasping Mechanism
Use two spur gears of the same diameter in mesh so that when the driver gear is reversed, the driven gear is also reversed. You can obtain a working piece grasping mechanism by utilizing this motion. Work pieces of various sizes can be accommodated by adjusting the opening angle of the grasping claw resulting in a versatile grasping mechanism design. - Intermittent Motion Mechanism
There is the Geneva mechanism as an intermittent motion mechanism. However, because of need for the specialized mechanical components, it is high priced. By using the missing teeth gears, a low cost and simple intermittent mechanism can be obtained.
By missing teeth gear, we mean a gear in which any number of gear teeth have been removed from their roots. The gear which is mated to the missing teeth gear will rotate as long as it is meshed together but will stop as soon as it encounters the missing teeth section of the driving gear. However, it has the disadvantage of shifting when external force is applied while the gears are disengaged. In these cases, it is necessary to maintain its position by means such as using a friction brake. -
Special Power Transmission Mechanism
By mounting a one-way clutch (a mechanism that allows rotational motion in one direction only) in one stage of a gear train of a gear speed reducer, you can create a mechanism which transmits motion in one direction but idles in reverse.
By using this mechanism, you can create a system that operates a motor when the electric power is on, but when the power is cut, it moves the output shaft by a spring force.
By internally mounting a spring (torsion coil spring or spiral spring) that winds in the rotational direction in a gear train, the speed reducer is operated as the spring is wound. Once the spring is completely wound, the motor is stopped and the electromagnetic brake built into the motor holds this position.
When the electricity is cut, the brake is released and the spring force will drive the gear in the opposite direction to when the motor was driving. This mechanism is used to close valves when the power is lost (emergency) and is called “spring return type emergency shutoff valve”.
Why is it difficult to obtain needed gears ?
There is no standard for the gear itself
Gears have been used worldwide since ancient times in many applications and are representative components of machine elements. However, as far as the precision class of gears, there are industrial standards in various countries such as AGMA(US), JIS(Japan), DIN(Germany), etc. On the other hand, there are no standards with regard to factors which ultimately specifies [the gear itself] such as its form, size, bore diameter, material, hardness, etc. As a result, there is no unified approach but it is a collection of the actual gear specifications decided by the individual designers that suits the design of their machines or those decided by the individual gear manufacturers.
There is a diversity of gear specifications
As mentioned above, there is a diversity of gear specifications. With the exception of very simple gears, it is not an overstatement to say that there are as many kinds as there are places where gears are used. For example, among many gears, when the pressure angle, tooth pitch and number of teeth specifications are matched, there are many other specifications that define gears such as bore size, face width, heat treatment, final hardness, surface roughness after grinding, existence of shaft, etc. It can be said that the possibility of two gears being compatible is low. This is one of the reasons why (when a gear breaks, for example) it is difficult to obtain a replacement gear.
Cannot obtain the desired gears
Sometimes it occurs that you cannot obtain a replacement gear for a worn out or broken one at the place the machine is being used. In this case, most of the time, there is no problem if there is a manual or a parts list for the machine that contains the drawing necessary for the gear's manufacture. There is also no problem if it is possible to contact the machine's manufacturer and that the maker can supply the needed gear. Unfortunately, in many cases :
- The machine's manual does not show the drawing of the gear by itself
- It is not possible to obtain only the gear from the machine's manufacturer, etc
For such reasons, it is difficult to obtain the needed gear. In these cases, it becomes necessary to make the manufacturing drawing of the broken gear. This is often difficult without specialized technical gear knowledge. The situation is often similarly difficult for gear manufacturers due to insufficient data for the gear. Also, to create the drawing from the broken gear requires great deal of engineering manpower and this raised the question of who will be burdened with this cost.
When only one gear is needed, the production cost is high
When the machine using a gear is mass produced, then so is the gear which is made to a certain production lot size, spreading the unit cost of the gear by taking advantage of the economy of scale. On the other hand, users utilizing the machine after it has been manufactured and when one or two gears need replacement, they often face a high production cost making the final repair cost at times very expensive. In short, the difference in the two production methods (mass production or small lot production) has a large effect on the cost of the gear. For example, a purchase of 300 gears in one shot for a new machinery production project (making 300 gears in one lot) compared to buying one replacement gear later (with the production lot of 1 piece) has a tremendous difference in manufacturing unit cost. This is the same situation at the design stage of a new machine when one gear is needed for the prototype with the same high cost.
Possibility of using standard gears
When designing a new machine, if the specifications of the gears used can be matched to those of the gear manufacturer's standard gears, the problems mentioned above can be solved. By this method :
- You can avoid the step of designing new gears during the design of a machine
- You can utilize 2D/3D CAD models, printable part drawings, strength calculations, etc. provided by the gear maker
- Even if you need only one gear as a trial, the standard gears are normally mass produced by the gear maker and are reasonably priced
Also, when a gear in a machine in use needs replacement, if its specifications are similar to those of a gear maker's, it may be possible to interchange it with a standard gear by itself or a standard gear with a secondary operation. In this situation also, it may be possible to avoid the inconvenience of doing the following tasks :
- Look for drawings
- Create new drawings
- Look for a contractor to make the gear
- Accept the high cost of one piece production


