Transmission and Planetary gear mechanism
Many “gears” are used for automobiles, but they are also used for many other machines. The most typical one is the “transmission” that conveys the power of engine to tires. There are broadly two roles the transmission of an automobile plays : one is to decelerate the high rotation speed emitted by the engine to transmit to tires; the other is to change the reduction ratio in accordance with the acceleration / deceleration or driving speed of an automobile.
The rotation speed of an automobile’s engine in the general state of driving amounts to 1,000 – 4,000 rotations per minute (17 – 67 per second). Since it is impossible to rotate tires with the same rotation speed to run, it is necessary to lower the rotation speed utilizing the ratio of the number of gear teeth. Such a role is called deceleration; the ratio of the rotation speed of engine and that of tires is called the reduction ratio.
Then, why is it necessary to change the reduction ratio in accordance with the acceleration / deceleration or driving speed ? This is because substances need a large force to start moving however they do not require such a large force to keep moving once they have started to move. Automobile can be cited as a good example. An engine, however, by its nature can’t so finely change its output. Therefore, one adjusts its output by changing the reduction ratio utilizing a transmission.
The transmission of motive power through gears very much resembles the principle of leverage (a lever). The ratio of the number of teeth of gears meshing with each other can be deemed as the ratio of the length of levers’ arms. That is, if the reduction ratio is large and the rotation speed as output is low in comparison to that as input, the power output by transmission (torque) will be large; if the rotation speed as output is not so low in comparison to that as input, on the other hand, the power output by transmission (torque) will be small. Thus, to change the reduction ratio utilizing transmission is much akin to the principle of moving things.
Then, how does a transmission change the reduction ratio ? The answer lies in the mechanism called a planetary gear mechanism.
A planetary gear mechanism is a gear mechanism consisting of 4 components, namely, sun gear A, several planet gears B, internal gear C and carrier D that connects planet gears as seen in the graph below. It has a very complex structure rendering its design or production most difficult; it can realize the high reduction ratio through gears, however, it is a mechanism suited to a reduction mechanism that requires both small size and high performance such as transmission for automobiles.
Graph 17.1: Structure of planetary gear mechanism
Planetary gear mechanisms have a characteristic of being able to change the reduction ratio by choosing which of the components is to be fixed.
For example, suppose internal gear C is fixed, the input axis is connected to sun gear A, and the output axis carrier D. When sun gear A rotates one time,
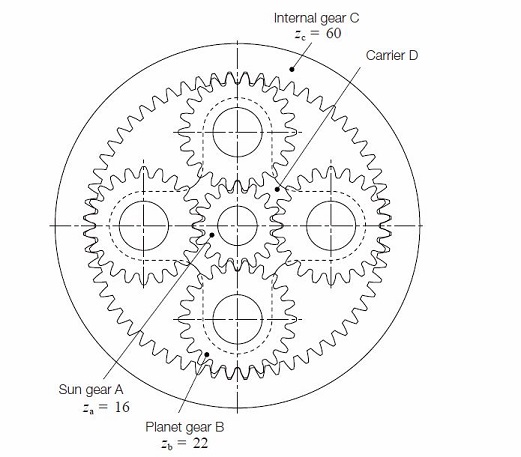
planet gear B will rotate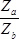 times.
If internal gear C is not fixed, but carrier D is fixed instead, when planet gear B rotates one time, internal gear C will rotate
times.
If internal gear C is not fixed, but carrier D is fixed instead, when planet gear B rotates one time, internal gear C will rotate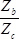 times.
This means that when sun gear A rotates one time, internal gear C will rotate
times.
This means that when sun gear A rotates one time, internal gear C will rotate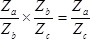 times.
But since in actuality internal gear C is fixed, and carrier D will be in motion, the whole planetary gear mechanism is to be considered rotated
times.
But since in actuality internal gear C is fixed, and carrier D will be in motion, the whole planetary gear mechanism is to be considered rotated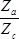 times, only.
Then sun gear A will rotate
times, only.
Then sun gear A will rotate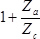 times and
times and
carrier D 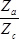 times, leading to the reduction ratio of
times, leading to the reduction ratio of 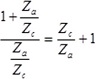 .
.
Next, suppose carrier D is fixed, the input axis is connected to sun gear A, and the output axis planet internal gear C. In this case, planet gear B will rotate only for transmitting the motive power as a non-vital gear. In addition, since internal gear C will rotate in the direction reverse to sun gear A, the reduction ratio will be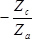 .
.
Thus, by fixing and rotating the components in a gear mechanism, a transmission changes the reduction ratio without requiring a large mechanism.
Appendix – Planetary gear
This article is reproduced with the permission.
Masao Kubota, Haguruma Nyumon, Tokyo : Ohmsha, Ltd., 1963.
Planetary gear is the gear train composed of the gear (sun gear) which is fixed or rotates around the fixed center and the gear (planetary gear) rotates around the center which revolves around the sun gear. Pic 12.9 shows the simplest planetary gear. When the gear A (teeth number is α) is fixed (fixed sun gear) and the arm C rotate toward ωc, and the gear B (planetary gear, teeth number is b) rotates while revolving.
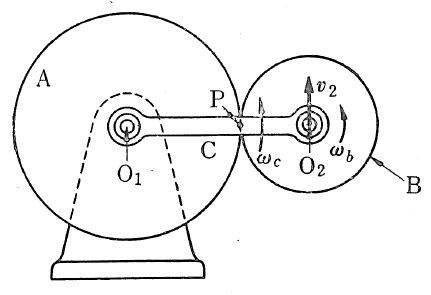
Pic 12.9 Very simple planetary gear
Assuming the angular speed to the space where it revolves as ωb, let us obtain the relationship between ωb and ωc. Firstly, the speed v2 at the center O2 of the planetary gear B equals to ωc by O1O2. On the other hand, the point P is fixed because the gear A doesn’t rotate. As the gear B rotate around the point B in the angular speed at a rate of ωb, v2 = ωb by PO2. Therefore,
ωb /ωc = O1O2 / PO2 = a + b / b
(12.3)
Alternatively, you can consider as follows: consider the rotation when the gear A and B is meshing while the arm C fixes as a normal meshing, then give A the reverse rotation while A, B and C are mutually fixed. Then, the rotation of A becomes 0 (fixed) and the rotation of B and C is as shown in the table 12.1.
Table 12.1
| A | B | C | ||
| Against C | 1 | – a / b | 0 | |
| With C | -1 | -1 | -1 | (+ |
| 0 | – (1+a/b) | -1 |
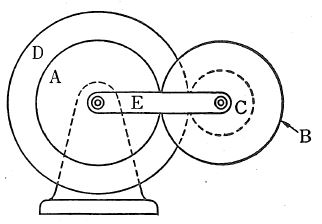
Pic 12.10 Turn-back planetary gear with external gear
Pic 12.10 shows the typical turn-back planetary gear which turns back and transmits rotation from the fixed sun gear to the concentric rotating sun gear through the planetary gear. You can obtain large speed ratio using small machine. This mechanism is used for reduction / speed-up gear. In the picture above, meshing is the sun gear A -> the planetary gear B -> the planetary gear C (coupled with the gear B) -> the sun gear D (concentric to but not coupled with the gear B) and the gear A is fixed, while the arm E rotates.
To obtain the speed ratio, firstly fix the arm E and obtain the rotation of each gear for one rotation of the gear A, then calculate the number of rotation of each gear by giving the gear A -1 revolution as in the table 12.2.
Table 12.2
| A | B | C | D | E | ||
| Against E | + 1 | – a / b | – a / b | ac / bd | 0 | |
| With E | -1 | –1 | -1 | –1 | -1 | (+ |
| 0 | – (1+a/b) | – (1+a/b) | – (1-ac/bd) | -1 |
Therefore, if the angular speed of the arm is ωe, the angular speed ωd of the sun gear D is expressed by using the following formula :
ωd = – (ac / bd – 1) ωe
(12.4)
In this case, D inversely rotates to E when ac>bd, D and E synchronously rotate when ac<bd, and D doesn’t rotate when ac=bd. If ac and bd are nearly same value, 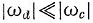 and you can obtain a large speed ratio.
and you can obtain a large speed ratio.
There are various forms of planetary gear in addition to above, such as one with internal gear as in pic 12.11 and table 12.3, or with bevel gear as in pic 12.12.
When any of external gears is replaced with internal gear, use the negative sign for pitch circle’s radius in the formula for the speed ratio.
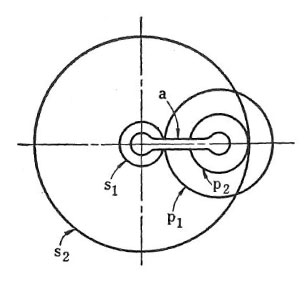
Pic 12.11 Turn-back planetary gear with internal gear
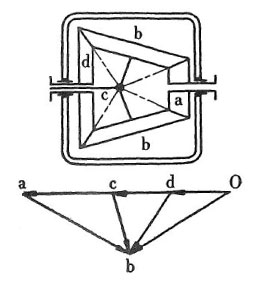
Pic 12.12 Planetary gear with bevel gear
Table 12.3
| fixed gear | driving gear | driven gear | rotation number of s1 | rotation number of s2 | rotation number of a | rotation number of axis of p1, p2 |
| s2 | a | s1 | p2s1+p1s2/p2s1 | 0 | 1 | s2/p2 |
| s1 | a | s2 | 0 | p2s1+p1s2/p1s2 | 1 | s1/p1 |
| s2 | s1 | a | 1 | 0 | p2s1/p2s1+p1s2 | p2s1/p2s1+p1s2 * s2/p2 |
| s1 | s2 | a | 0 | 1 | p1s2/p2s1+p1s2 | p1s2/p2s1+p1s2 * s1/p1 |
Related links :
Gear Systems



