Click Here : KHK's Anti-backlash Gears
For smooth rotation of meshed gears, backlash is necessary. Backlash is the amount by which a tooth space exceeds the thickness of a gear tooth engaged in mesh. Backlashes are classified in the following ways.
6.1 Types of Backlashes
(1) Circumferential Backlash ( j t )
Circumferential Backlash is the length of arc on the pitch circle. The length is the distance the gear is rotated until the meshed tooth flank makes contacts while the other mating gear is held stationary.
(2) Normal Backlash ( j n )
The minimum distance between each meshed tooth flank in a pair of gears, when it is set so the tooth surfaces are in contact.
(3) Angular Backlash ( j
θ)
The maximum angle that allows the gear to move when the other mating gear is held stationary.
(4) Radial backlash ( j r )
The radial Backlash is the shrinkage (displacement) in the stated center distance when it is set so the meshed tooth flanks of the paired gears get contact each other.
(5) Axial Backlash ( j x )
The axial backlash is the shrinkage (displacement) in the stated center distance when a pair of
bevel gears
is set so the meshed tooth flanks of the paired gears contact each other.
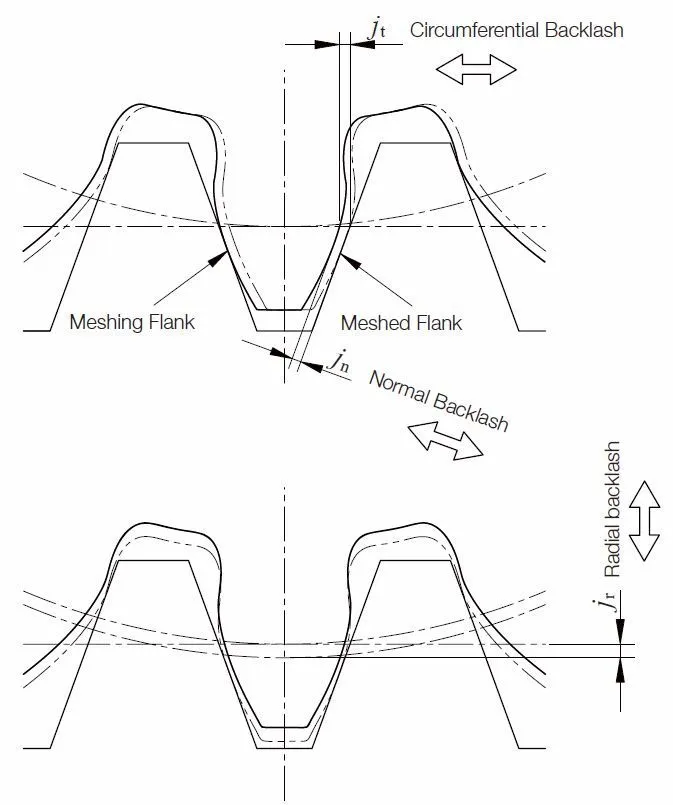
Fig. 6.1 Circumferential Backlash – Normal Backlash and Radial Backlash
6.2 Backlash Relationships
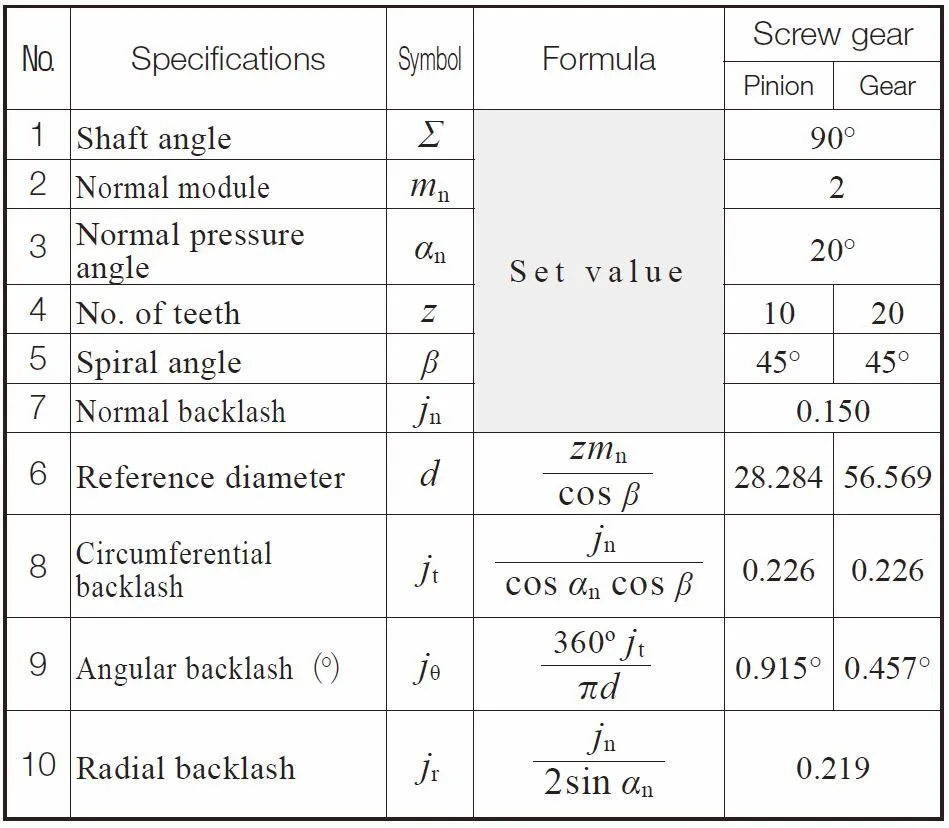
Table 6.1 reveals relationships among backlashes and the fundamental equations. While bevel gears are of cone shaped gears, axial backlash is considered instead of radial backlash.
Table 6.1 Relationships among backlashes
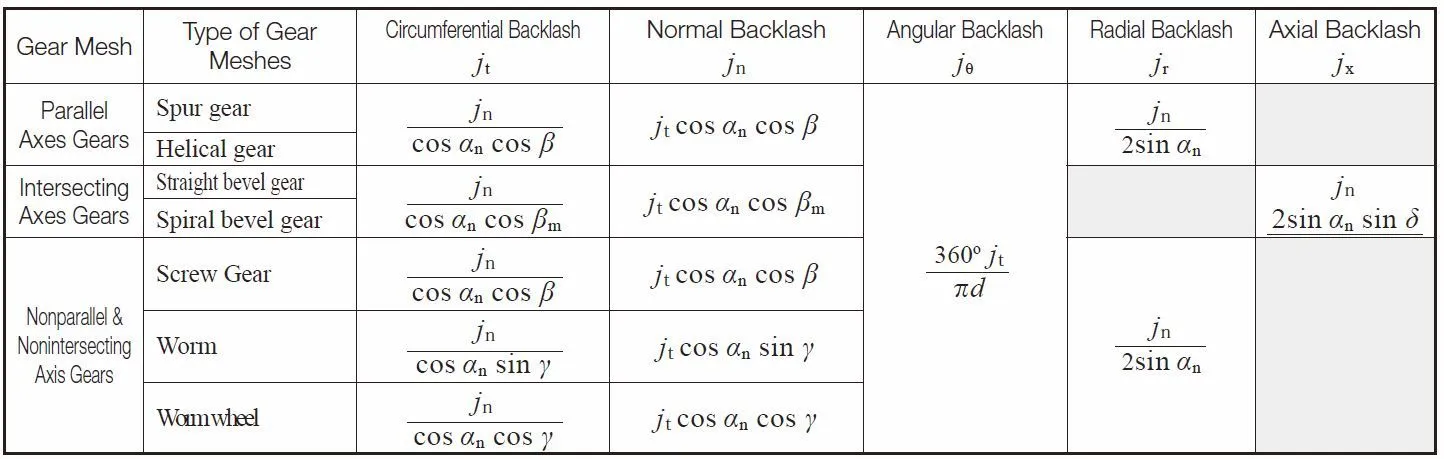
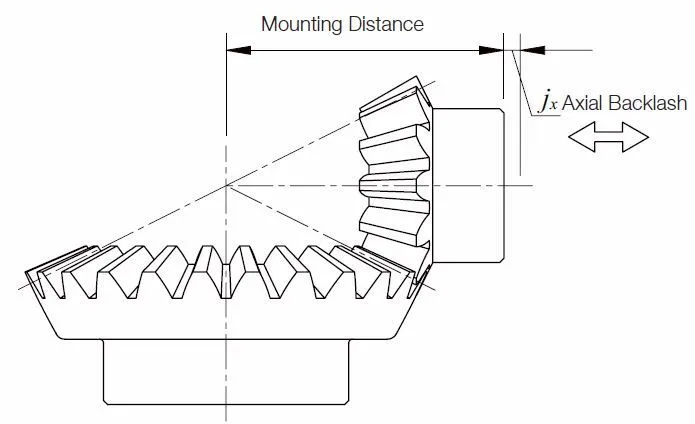
Fig. 6.2 Axial Backlash of a Bevel Gear
(1) Backlash of Parallel Axes Gear Mesh
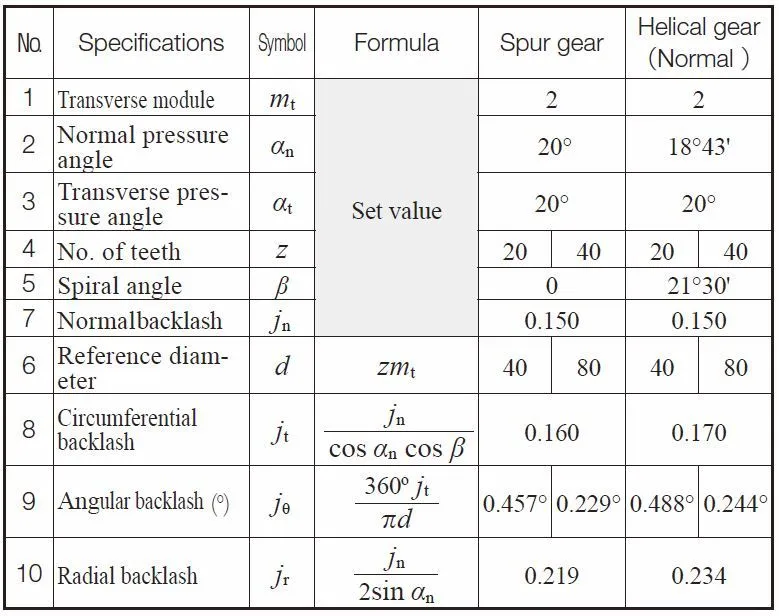
Table 6.2 shows calculation examples for backlashes and the center distance of
spur gear
and
helical gear
meshes. By adjusting the center distance (radial backlash), backlash can be controlled.
Table 6.2 Spur and Helical Gear Mesh
(2) Backlash of Intersecting Axes Gear Mesh
Table 6.3 shows calculation examples for backlashes and the mounting distance of bevel gear meshes. The common way to control backlash of bevel gear meshes is to adjust the mounting distance (axial backlash) by adding shims. When adjusting the mounting distance, it is important to keep proper tooth contact in consideration of the gears and pinions in balance.
Table 6.3 Bevel Gear Mesh
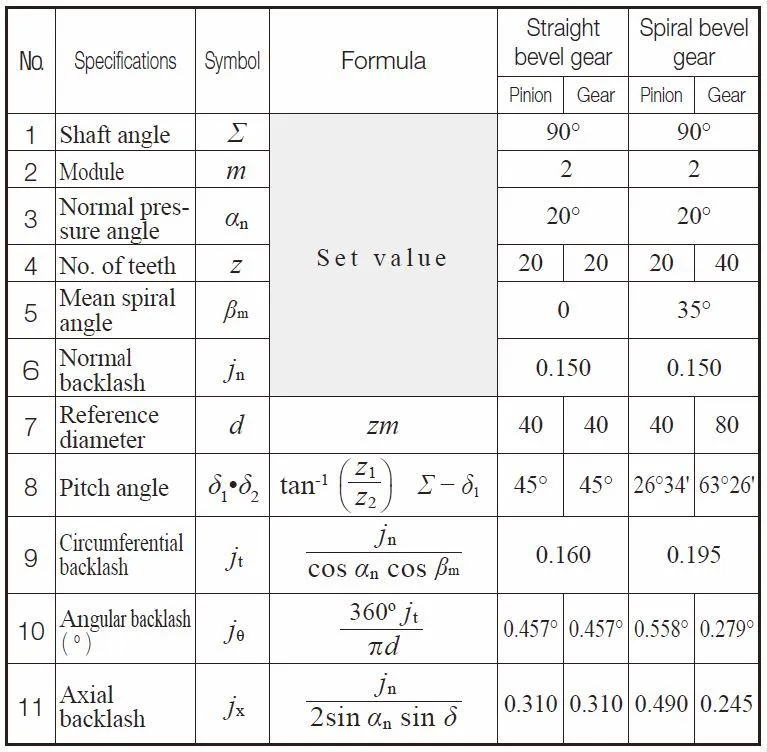
(3) Backlash of Nonparallel and Nonintersecting Axes Mesh
Table 6.4 shows calculation examples for backlashes and the mounting distance of
worm gear
meshes.
A Worm gear pair has a different circumferential backlash for each drive and driven gear (worm and wheel) and it is a feature of a worm gear pair.
Table 6.4 Worm Gear Pair Meshes
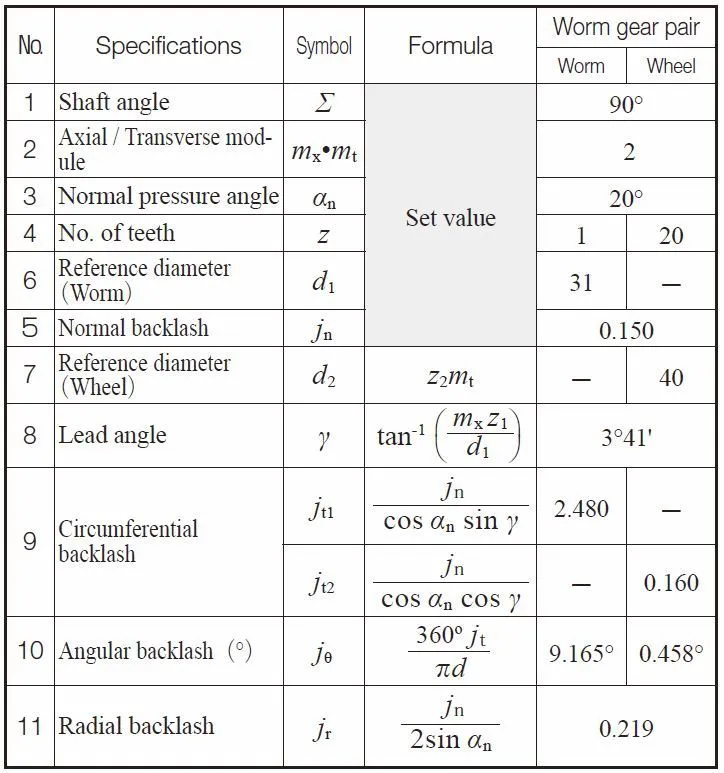
Table 6.5 Calculation example for backlash screw gear meshes.
Table 6.5 Screw Gear Mesh
6.3 Tooth Thickness and Backlash
There are two ways to produce backlash. One is to enlarge the center distance. The other is to reduce the tooth thickness. The latter is much more popular than the former. We are going to discuss more about the way of reducing the tooth thickness.
In SECTION 5, we have discussed the standard tooth thickness s1 and s2. In the meshing of a pair of gears, if the tooth thickness of pinion and gear were reduced by Δs1 and Δs2, they would produce a backlash of Δs1 and Δs2 in the direction of the pitch circle. Let the magnitude of Δs1 and Δs2 be 0.1., We know that α = 20 degrees, then :
![]()
We can convert it into the backlash on normal direction jn:
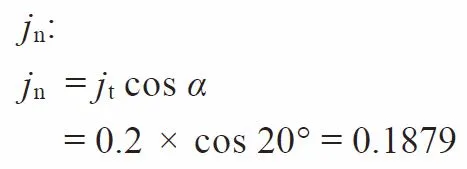
Let the backlash on the center distance direction be jr, then:
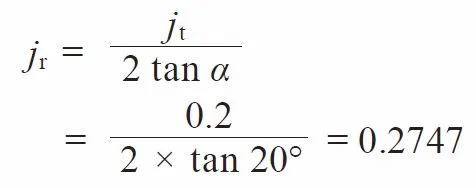
These express the relationship among several kinds of backlashes. In application, one should consult the JIS standard. There are two JIS standards for backlash – one is JIS B 1703-76 (Suspended standard) for spur gears and helical gears, and the other is JIS B 1705-73 for bevel gears. All these standards regulate the standard backlashes in the direction of the pitch circle jt or jtt. These standards can be applied directly, but the backlash beyond the standards may also be used for special purposes. When writing tooth thicknesses on a drawing, it is necessary to specify, in addition, the tolerances on the thicknesses as well as the backlash.
For example :
![]()
Since the tooth thickness directly relates to backlash, the tolerances on the thickness will become a very important factor.
6.4 Gear Train and Backlash
The discussions so far involved a single pair of gears. Now, we are going to discuss two stage gear trains and their backlash. In a two stage gear train, as Figure 6.3 shows, jt1 and jt4 represent the backlashes of first stage gear train and second stage gear train respectively.
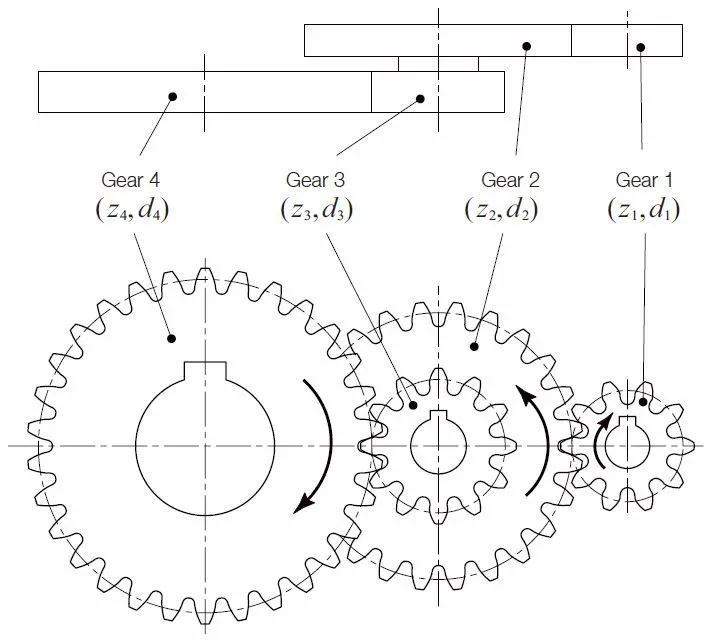
Fig.6.3 Overall accumulated backlash of two stage gear train
If number one gear were fixed, then the accumulated backlash on number four gear jtT4 would be as follows:

This accumulated backlash can be converted into rotation in degrees:
![]()
The reverse case is to fix number four gear and to examine the accumulated backlash on number one gear jtT1.
![]()
This accumulated backlash can be converted into rotation in degrees:
![]()
6.5 Method of Reducing Backlash (Zero Backlash Gears)
Low backlash or zero-backlash is the performance required for high-precision gear applications. In order to meet special needs, precision gears are used more frequently than ever before. This section introduces methods of reducing or eliminating backlash.
(1) Use of Gears with less tooth thinning (Common Method)
By processing gears which have less amount of tooth thinning than common gears, and by using them with the center distance or mounting distance fixed at normal values, it enables to reduces backlash. This method cannot be used to make the backlash zero, but it is the most simple way and applicable to many types of gears. If you use the gear with low runout, you can reduce the backlash variation. Zero-backlash is concerned. It should be considered carefully that the gear may not rotated smoothly if the generated backlash value is zero.
(2) Use of gears adjustable for small backlash
A method to use gears to adjust for low backlash. Zero-backlash can not be generated with this method.
(a) Control backlash by adjustment of the center distance
This method can be applied to spur, helical, screw and worm gears. By shortening the center distance of the gear, this enables adjustment of the radial plays and reduce the backlash. The adjustment of the center distance is complicated.
(b) Control backlash by adjustment of mounting distance
For bevel gears, shortening of the mounting distance of the gear, enables to control axial plays and reduce the backlash. The adjustment of the center distance is rather complicated, if the mounting distance of only one of the paired bevel gears is adjusted, this creates bad tooth contact. The mounting distance of each meshed gear should be adjusted with equally., this method is generally made by adjusting shims.
(c) Control backlash by separating the gear into two parts
This method is applicable for most types of gears. By separating a gear in two parts, and by adjusting and fixing the phase relationships between the tooth position of each, generates low backlash. This is shown in Fig. 6.4.
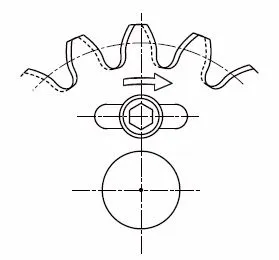
Fig. 6.4 Gear separated in two parts. (Fixed)
For helical gears or worm gears, there is a way to adjust the phase relationships between the tooth position of each meshed gear by moving one of the paired gears (1) in an axial direction. Fig. 6.5 shows the basis.
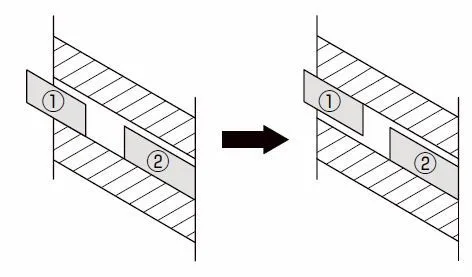
Fig. 6.5 Backlash Adjustment of Helical Gear
(d) Tapered gears (Spur gear and tapered
gear racks
)
Tapered gears are also called conical gears. Since tapered gears are a cone shaped gear having continuously-shifted teeth, the tooth profile/tooth thickness are continuously transformed. Fig. 6.6 shows the tooth profile of a tapered spur gear. Since the tooth thickness of the meshed tooth varies if the taper gear is moved in axial direction, this enables you to adjust backlash. The shim adjustment is a simple and easy way to move the tapered gear in axial direction.
Unlike bevel gears, moving the tapered gear in axial direction involves no change in tooth contact and this is an advantage of tapered gears.
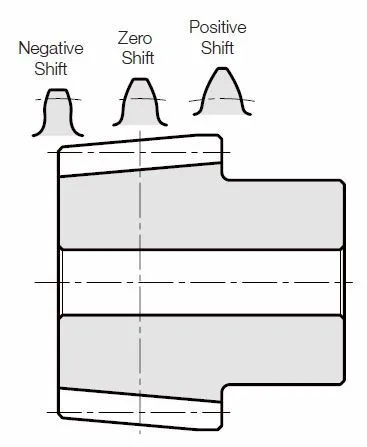
Fig. 6.6 Tooth Profile of Tapered Spur Gear
(e) Duplex Lead Worm Gear Pair
A Duplex lead worm gear differs in module between the right and left tooth surface. While the pitch of the right and left tooth surface also differs, the tooth thickness varies continuously. By shifting the worm axially, the tooth thickness at the working point varies, and can be used to adjust the backlash of the duplex lead worm gears. There are some methods to adjust the worm in the axial direction. The simple and secure way is shim adjustment, in the same way as any other type of gears. Zerobacklash is not favorable, as the worm gear mesh requires a certain amount of backlash to avoid the depletion of lubricant on the tooth surface.
Figure 6.7 presents the basic concept of a duplex lead worm gear pair. (For more detail, please see page 418)
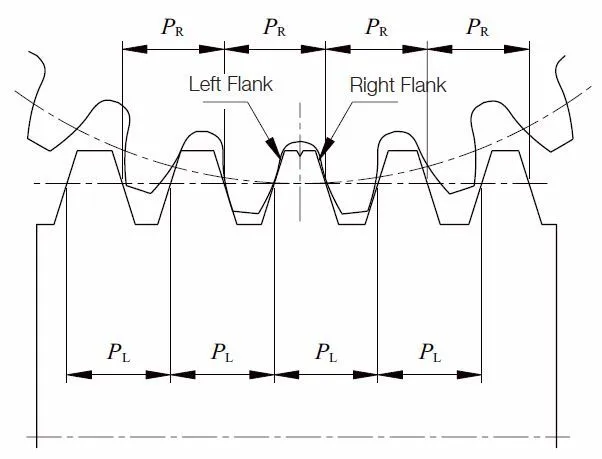
Fig. 6.7 Basic Concept of the Duplex Lead Worm Gear
(3) Gears which have Zero-Backlash
This type of gear has a structure that can forcibly remove backlash by external force. While this structure involves double flank meshing, it should be carefully maintained to avoid the depletion of lubricant. This structure is not suitable for gears, which have a large amount of slippage on the tooth surface when transmitting power, such as worm gear or screw gears. If the depletion of the lubricant occurs on the tooth surface causing large slippage, there is danger of abrasion.
Scissors Gear with Zero Circumferential Backlash
By applying spring force to the tightly held teeth of the mating gear, with the gear separated in two parts, the backlash is removed. Figure 6.8 shows the structure.
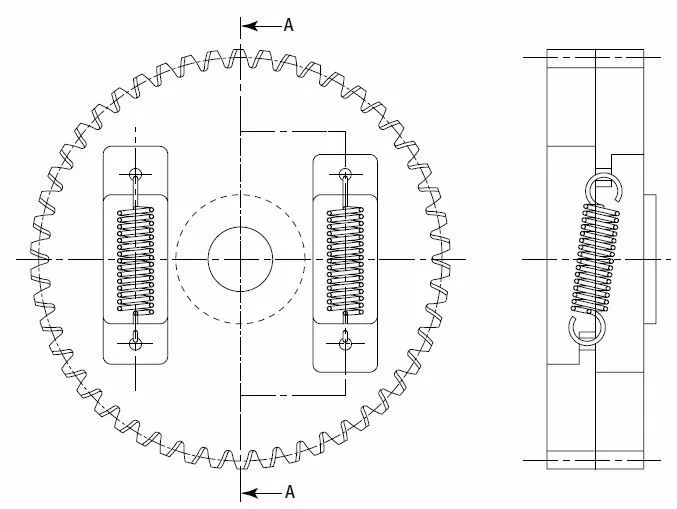
Fig. 6.8 Scissors Gear (with Coil Springs)
相关链接 - 齿轮的侧隙



