Gears cannot work singularly to transmit power. At least two or more gears must be meshed to work. This section introduces a simple gear train “Single-Stage Gear Train” and its use in pairs for a “Two-Stage Gear Train”.
2.1 Single-Stage Gear Train
A pair of meshed gears is the basic form of a single-stage gear train. Figure 2.1 shows forms of the single-stage gear train.
In a single-stage gear train, which consists of z1 and z2 numbers of teeth on the driver and driven gears, and their respective rotations, n1 & n2. The speed ratio is :
Speed Ratio i = z2 / z1 = n1 / n2 (2.1)
Gear trains can be classified by three types, in accordance with the value of the speed ratio i :
Speed ratio i < 1, Increasing : n1 < n2
Speed ratio i = 1, Equal speeds : n1 = n2
Speed ratio i > 1, Reducing : n1 > n2
For the very common cases of spur gear and bevel gear meshes, see Figures 2.1 (A) and (B), the direction of rotation of driver and driven gears are reversed. In the case of an internal gear mesh, see Figure 2.1 (C), both gears have the same direction of rotation. In the case of a worm mesh, see Figure 2.1 (D), the rotation direction of z2 is determined by its helix hand.
Fig. 2.1 Single-Stage Gear Trains
(A) A Pair of Spur Gears
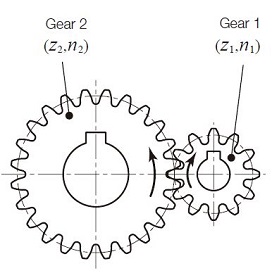
(B) Bevel Gears
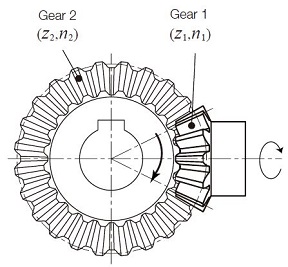
(C) Spur Gear and Internal Gear
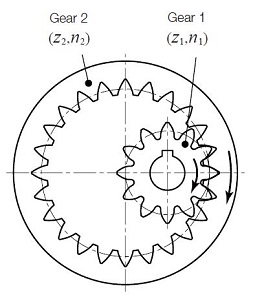
(D) Worm Gear Pair
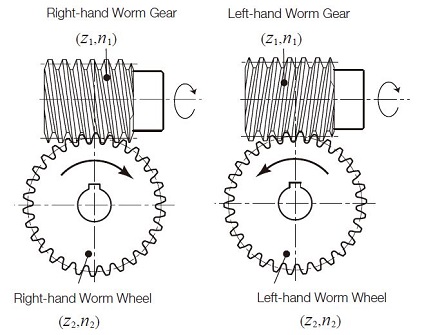
In addition to these four basic forms, the combination of a rack and pinion can be considered as a specific type. The displacement of a rack, for rotation θ of the mating pinion is :

Where:
πm is the reference pitch
z1 is the number of teeth of the pinion
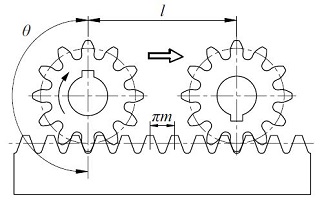
Fig. 2.2 Rack and Pinionw
2.2 Two-Stage Gear Train
A two-stage gear train uses two single-stages in series. Figure 2.3 represents the basic form of an external gear two-stage gear train. Let the first gear in the first stage be the driver. Then the speed ratio of the two-stage gear train is :
Speed Ratio i = z2 / z1 X Z4 / Z3 = n1 / n2 x n3 / n4 (2.3)
In this arrangement, n2 = n3
In the two-stage gear train, Fig. 2.3, Gear 1 rotates in the same direction as gear 4.
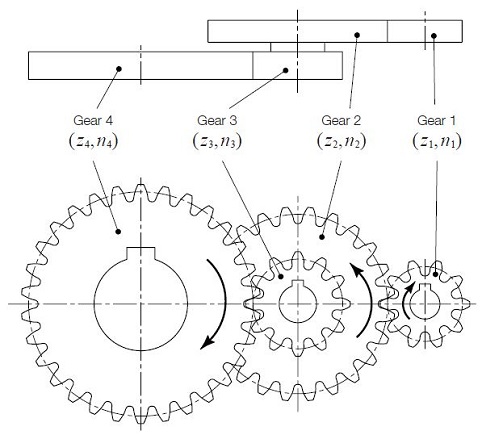
Fig. 2.3 Two-Stage Gear Train
If gears 2 and 3 have the same number of teeth, then the train is simplified as shown in Figure 2.4. In this arrangement, gear 2 is known as an idler, which has no effect on the speed ratio. The speed ratio is then :
Speed ratio i = z2 / z1 x z3 / z2 = z3 / z1 (2.4)
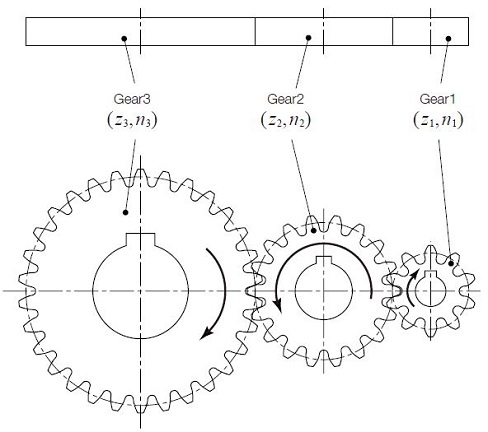
Fig. 2.4 Single-stage gear train with an idler
Table 2.1 introduces calculation examples for two-stage gear trains in Fig.2.3.
Table 2.1 Speed Ratio of Two-Stage Gear Trains
| No. | Term | Symbols | Formula | Calculation Example | |
| Pinion | Gear | ||||
| 1 | Number of Teeth (First Gear) |
z1, z2 | Set Value | 10 | 24 |
| 2 | Number of Teeth (Second Gear) |
z3, z4 | 12 | 30 | |
| 3 | RPM (Gear 1) | n1 | 1200 | – | |
| 4 | Speed ratio (First Stage) |
i1 | z2 / z1 | 2.4 | |
| 5 | Speed ratio (Second Stage) |
i2 | z4 / z3 | 2.5 | |
| 6 | Final Speed Ratio | i | i1 x i2 | 6 | |
| 7 | RPM (Gear 2 and 3) |
n2 | n1 /i1 | 500 | |
| 8 | RPM (Gear 4) | n4 | n1 / i | – | 200 |
RPM: Revolution per Minute
Set value here stands for the values pre-designated by the designer
Appendix – Gear train
This article is reproduced with the permission.
Masao Kubota, Haguruma Nyumon, Tokyo : Ohmsha, Ltd., 1963.
A mechanism with two or more gears meshed in series and its axes interlocked by a proper link to transmit power and to increase/decrease rotary speed is called a gear train. Two input motions can be put into one interlocked gear train, but three or more input motions cannot be put. Among those two input motions, you can impart an arbitrary motion to move one element against a fixed space, but in fact, you can only fix the element or rotate the element around the revolute pair. Another input motion is limited to one which causes a locked relative interlocking mechanism.
The relative motion of the gears whose axes are parallel such as spur gears and helical gears is represented by the rolling contact of its pitch circle (the radius of the pitch circle is proportionate to number of teeth if the module is constant). Therefore, the circumferential speed at the pitch point (contact point of pitch circle) is common to both gears, and the relation of rotary speed of each gear in a fixed support gear train is easily determined by taking advantage of the characteristics.
When the support frame rotates, the relationship of speed can be determined by drawing a vector diagram of rotary speed, taking advantage of the pitch point at the momentary center of relative motion of both gears. Alternatively, you can determine the relationship of rotary speed by superposition of the relative motions considered in series. In case of bevel gears, relative motion is represented by the rolling contact of the pitch cone (sine of pitch cone’s half apex angle is proportionate to number of teeth if the module is constant) because the shafts intersect. Therefore the rotary speed can be represented by a vector of direction of the rotary shaft. In this case, the contact line of the pitch cone becomes the instantaneous axis of relative motion.
Related Links :
齿轮系的传动比和旋转方向
Know about rotational directions and numbers of rotation of gears



