University Collaboration – Free Standard Gears for Humanoid Robot Research (Click Here)
KHK Gears supports academic research on humanoid robots by providing our standard gears free of charge. We welcome technical collaboration and information exchange on gear applications.
2. Basic Gear Terminology and Calculation / Let’s learn the basics of Basic Gear Technology !
Gear size, pressure angle, number of teeth…we introduce the basic terminology, measurement, and relational expressions necessary to understand basic gear technology.
Comparative Size of Gear-Teeth
Using ISO (International Organization for Standardization) guidelines, Module Size is designated as the unit representing gear tooth-sizes. However, other methods are used too.
Module (m)
m = 1 (p = 3.1416)
m = 2 (p = 6.2832)
m = 4 (p = 12.566)
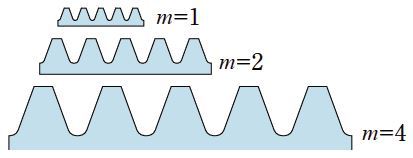
Fig.2.1 Tooth Profiles of Racks
If you multiply Module by Pi, you can obtain Pitch (p). Pitch is the distance between corresponding points on adjacent teeth.
p = Pi x Module = πm (2.1)
Calculation Example
What is the pitch size (p) of the Gear with module m = 3 ?
p = πm = 9.4248CP (Circular Pitch)
Circular Pitch (CP) denotes the reference pitch (p).
For instance, you can produce gears at an exact integral value, such as CP5/CP10/CP15/CP20.
Transformation from CP to Module
m = CP / π (2.2)
Calculation Example
CP10 is transformed to module as follows ;
m = 10 / 3.1416 = 3.1831DP (Diametral Pitch)
DP stands for Diametral Pitch.
By ISO standards, the unit Millimeter (mm) is designated to express length, however, the unit inch is used in the USA, the UK and other countries; Diametral Pitch is also used in these countries.
Transformation from DP to Module
m = 25.4 / DP (2.3)
Calculation Example
DP 8 is transformed to module as follows ;
m = 25.4 / 8 = 3.175Pressure Angle ( α )
Pressure angle is the leaning angle of a gear tooth, an element determining the tooth profile.
Recently, the pressure angle (α) is usually set to 20°, however, 14.5° gears were prevalent.
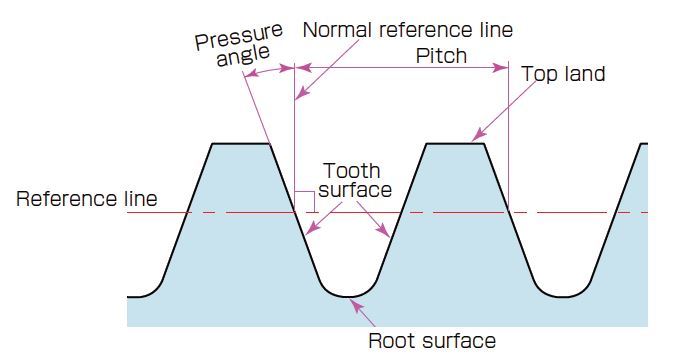
Fig.2.2 Normalized Tooth Profile of Reference
(Important Gear Terminology and Gear Nomenclature in Fig 2.2)
- Reference line
- Pressure angle
- Normal reference line
- Pitch
- Tooth surface
- Root surface
- Top land
Number of teeth
Number of teeth denotes the number of gear teeth.
They are counted as shown in the Figure 2.3. The number of teeth of this gear is 10.
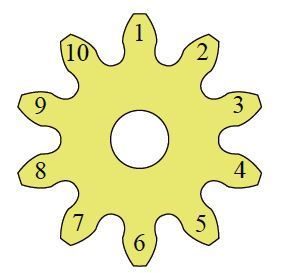
Fig. 2.3 Number of teeth
Module (m) , Pressure Angle (α) , and the Number of Teeth, introduced here, are the three basic elements in the composition of a gear. Dimensions of gears are calculated based on these elements.
Tooth Depth and Thickness
Tooth depth is determined from the size of the module (m). Introduced here are Tooth Profiles (Full depth) specified by ISO and JIS (Japan Industrial Standards) standards.
Please see Figure 2.4 below for explanations for Tooth depth (h) / Addendum (ha) / Dedendum (hf).
Tooth depth (h) is the distance between tooth tip and the tooth root.
h = 2.25 m
(= Addendum + Dedendum) (2.4)
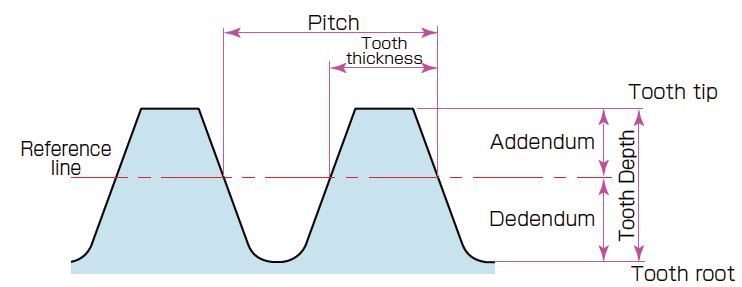
Fig. 2.4 Tooth Depth and Thickness
(Important Gear Terminology and Gear Nomenclature in Fig 2.4)
- Reference line
- Pitch
- Tooth thickness
- Addendum
- Dedendum
- Tooth Depth
- Tooth tip
- Tooth root
Addendum (ha) is the distance between the reference line and the tooth tip.
ha = 1.00 m (2.5)
Dedendum (hf) is the distance between the reference line and the tooth root.
hf = 1.25 m (2.6)
Tooth thickness (s) is basically half the value of pitch (p). * Pitch (p) = πm
s = πm / 2 (2.7)
Calculation Examples
The following are calculations of Tooth depth (h) / Addendum (ha) / Dedendum (hf) for a gear with module 2.
h = 2.25 m = 2.25 × 2 = 4.50ha = 1.00 m = 1.00 × 2 = 2.00
hf = 1.25 m = 1.25 × 2 = 2.50
In the previous pages, we introduced the basics of gears, including 'Module', 'Pressure Angle', 'Number of Teeth' and 'Tooth Depth and Thickness'. In this section we introduce the basic parts of Spur Gears (Cylindrical gears) and dimensional calculations.
Diameter of Gears (Size)
The size of gears is determined in accordance with the reference diameter (d) and determined by these other factors; the base circle, Pitch, Tooth Thickness, Tooth Depth, Addendum and Dedendum.
Reference diameter (d)
d = zm(2.8)
Tip diameter (da)
da = d + 2 m(2.9)
Root diameter (df)
df = d - 2.5 m(2.10)
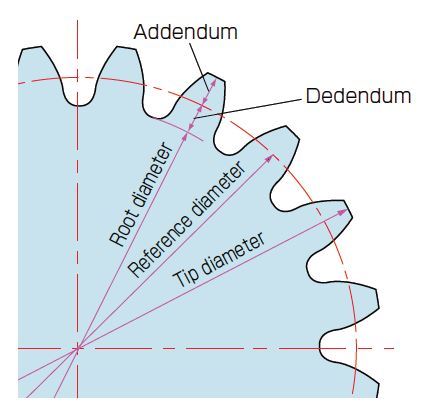
Fig.2.5 Diameter of Gears
(Important Gear Terminology and Gear Nomenclature in Fig 2.5)
- Addendum
- Dedendum
- Root diameter
- Reference diameter
- Tip diameter
The Addendum and dedendum circle introduced here are a reference circle that cannot be seen on a gear, as it is a virtual circle, determined by gear size.
Calculation Examples
The following are calculations of Reference diameter / Tip diameter / Root diameter for a spur gear with module (m) 2, and 20 teeth (z).
d = zm = 20 x 2 = 40da = d + 2 m = 40 + 4 = 44
df = d – 2.5 m = 40 – 5 = 35
Practice Test :
Spur Gear Specifications
Module (m) = 4
Number of teeth (z) = 40 (Pressure angle α = 20°)
| Reference diameter | d = | |
| Tip diameter | da = | |
| Root diameter | df = |
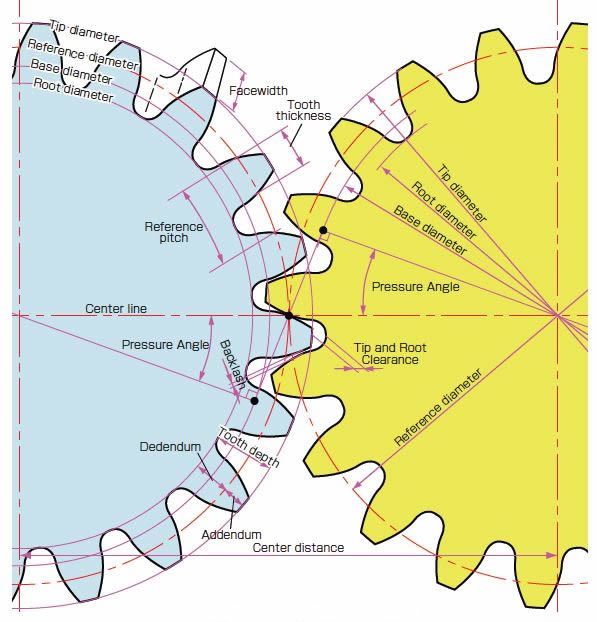
Fig. 2.6 Working Gear Nomenclature
(Important Gear Terminology and Gear Nomenclature in Fig 2.6)
- Tip diameter
- Reference diameter
- Base diameter
- Root diameter
- Face width
- Tooth thickness
- Reference pitch
- Center line
- Pressure Angle
- Backlash
- Tooth depth
- Addendum
- Dedendum
- Center distance
- Tip and Root Clearance
Table 2.1 Gear Symbols and Nomenclature
| Terms | Symbols | Terms | Symbols |
|---|---|---|---|
| Module | m | Tooth Thickness | s |
| Pressure Angle | α | Reference Diameter | d |
| Number of Tooth | z | Tip Diameter | da |
| Pitch | p | Root Diameter | df |
| Tooth Depth | h | Center Distance | a |
| Addendum | ha | Backlash | j |
| Dedendum | hf | Tip and Root Clearance | c |
Center Distance and Backlash
When a pair of gears are meshed so that their reference circles are in contact, the center distance (a) is half the sum total of their reference diameters.
Center distance (a)a = ( d1 + d2 ) / 2(2.11)
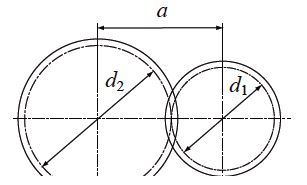
Fig. 2.7 Center distance
Gears can mesh as shown in the Figure 2.6, however, it is important to consider a proper backlash (play) so that the gears can work smoothly. Backlash is a play between tooth surfaces of paired gears in mesh.
Mating gears also have a clearance (play) vertical to tooth depth. This is called Tip and Root Clearance (c), the distance between tooth root and the tooth tip of mating gears.
c = 1.25 m - 1.00 m
= 0.25 m(2.12)
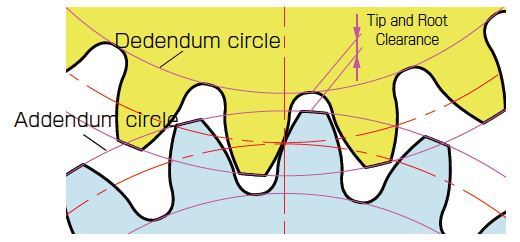
Fig. 2.8 Tip and Root Clearance
(Important Gear Terminology and Gear Nomenclature in Fig 2.8)
- Addendum circle
- Dedendum circle
- Tip and Root Clearance
Calculation Examples
The following are calculations for Center distance (a) and Tip and root clearance (c), when Module m = 2, Pinion z1 = 20, Gear z2 = 40
Reference diameter of Pinion d1 = 20 × 2 = 40
Reference diameter of Gear d2 = 40 × 2 = 80
Center distance a = (40 + 80) / 2 = 60
c = 0.25 × 2 = 0.5
Calculation Examples
Practice calculating the dimensions of gears.
| Terms | Symbols | Formula | Pinion | Gear |
|---|---|---|---|---|
| Module | m | - | 2.5 | |
| Pressure Angle | α | 20° | ||
| No. of Teeth | z | 15 | 30 | |
| Reference diameter | d | z m | 37.5 | 75 |
| Addendum | ha | 1.00 m | 2.5 | 2.5 |
| Dedendum | hf | 1.25 m | 3.125 | 3.125 |
| Tooth Depth | h | 2.25 m | 5.625 | 5.625 |
| Tip diameter | da | d + 2 m | 42.5 | 80 |
| Root diameter | df | d - 2.5 m | 31.25 | 68.75 |
| Center distance | a | d1 + d2 / 2 | 56.25 | |
Practice Test :
Calculations for the dimensions of gears.
| Terms | Symbols | Formula | Pinion | Gear |
|---|---|---|---|---|
| Module | m | - | 4 | |
| Pressure Angle | α | 20° | ||
| No. of Teeth | z | 12 | 60 | |
| Reference diameter | d | z m | ||
| Addendum | ha | 1.00 m | ||
| Dedendum | hf | 1.25 m | ||
| Tooth Depth | h | 2.25 m | ||
| Tip diameter | da | d + 2 m | ||
| Root diameter | df | d - 2.5 m | ||
| Center distance | a | d1 + d2 / 2 | ||
Helical Gear
Spur gears with helicoid teeth are called Helical Gears.
The majority of calculations for spur gears can be applied to helical gears too. This type of gear comes with two kinds of tooth profiles in accordance with the datum surface. (Figure 2.9)
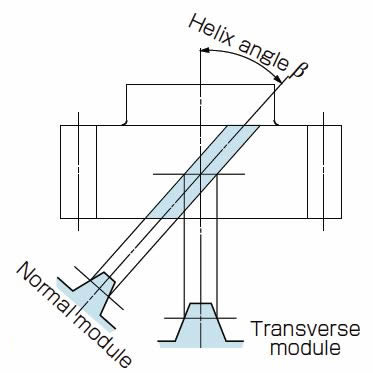
Fig. 2.9 Right-handed Helical Gear
(Important Gear Terminology and Gear Nomenclature in Fig 2.9)
(a) Transverse System (Transverse module / Pressure angle) * Transverse axis denotes the centerline of the gear.
(b) Normal System (Normal module / Pressure angle)
mt = mn / cos β(2.13)
Both systems are used in KHK Stock Gears.
Transverse System:KHG Grounding helical gears
Normal System:SH Helical gears
Reference diameter (d) of the helical gear with transverse system can be calculated from Equation (2.8).
Reference diameter (d) of the helical gear with normal system can be calculated from Equation (2.14).
d = zmn / cos β(2.14)
Calculation Examples
The following is a calculation for the Reference Diameter of a helical gear with:
Transverse module mt = 2, Number of teeth z = 30, Helix angle β = 15° (R)
Reference Diameter d = zmt = 30 × 2 = 60
The following is a calculation for the Reference Diameter of a helical gear with:
Normal module mn = 2, Number of teeth z = 30, Helix angle β = 15° (R)
Reference Diameter d = zmn / cos β = 30 × 2 / cos 15° = 62.117
Practice Test :
Helical Gear Specifications
Normal module ( mn ) = 4 Helix angle ( β ) = 15°
Transverse module mt =Troubleshooting Gears : Explanation of Terminology
Pitting
When the gear surface is repeatedly subjected to load and the force near the contact point exceeds the material's fatigue limit, fine cracks occur and eventually develop into separation of small pieces, thereby creating pits (craters).
Initial Stage Pitting
The initial cause comes from small convex portions of the gear surfaces contacting each other and the local load exceeding the fatigue limit. As gears are driven and surfaces become worn in, local convex portions disappear and the load is equalized and pitting stops.
Progressive Pitting
Even after gear surfaces are worn in and load is equalized, with time more pitting starts to occur and pits get enlarged.
(1) When an overload condition exists and the gear surface load exceeds the fatigue limit of the material.
(2) While being driven, the load distribution could become uneven across the gear face due to various parts' deflection causing the fatigue limit to become exceeded.
These are some of the possible reasons of progressive pitting.
Scoring
This is the condition in which the lubricant coating breaks down due to overheating of local contact areas causing the deterioration of the gear surface from metal to metal contact. It is possible for this condition to progress from moderate to break down.
Slotting
In the direction of gear sliding, groove like condition appears. This is part of abrasive wear and the following causes are possibilities.
(1) Wear from a solid foreign object larger than the oil film thickness getting caught in the gear mesh.
(2) Wear from a solid foreign object buried for some reason in the opposing gear tooth.
(3) Wear from the hard convex portion of the opposing gear tooth digging into the meshing gear.
Abrasion Wear
Wear that looks like an injury from abrasion or has the appearance of lapping. Below are some of the causes.
(1) Possible wear occurring from solid foreign objects mixed in the lubricant (such as metal wear debris, burr, scale, sand, etc.).
(2) Wear from the difference in hardness of two meshing gears in which the hard convex portion digs into the softer gear surface.
Adhesion Wear
Wear commonly occurring between metals in sliding contact. Wear reduction is related to type, pressure, speed, distance and lubrication.
A minute portion of the material in contact welds (adheres) and the wear mechanism comes from peeling off of these by shearing force.
Spalling
This refers to the symptom of relatively large metal chips falling off from the gear surface due to material fatigue below the surface from high load. The gear surface's concave part is large and the shape and the depth are irregular. Because the applied shear force exceeds the material's fatigue limit, fatigue cracks appear and grow leading to possible breakage of the tooth.
Excessive Wear
Wear from the gear surface being subjected to intense repeated metal to metal contact which occurs when the oil film is thin and the lubrication is insufficient relative to the load and surface roughness of the gear. This condition tends to occur when operating at very low speed and high load.
Overload Breakage
Breakage that comes from an unexpectedly heavy load for one or several action cycles (Normally, mistakes in design or manufacturing are not included). The fracture surface spreads fibrously from a starting point and indicates a sudden splitting. The cause is due to the load exceeding the tensile strength of the gear material. This may come from the prime mover, driven mechanism or breakage of bearings or other gears which could cause biting of teeth, sudden stop, or concentration of load due to irregular tooth contact.
Fatigue Breakage
This is the case in which the root portions of gear are subjected to a repeated load exceeding the material's fatigue limit. A fracture that starts in the corner of the gear root propagates until the tooth breaks. The fractured surface is relatively smooth and the starting point can often be recognized by the beach mark (shell pattern) around it.
Shear Breakage
This describes when a tooth separates from the body by shearing due to a one time extreme overload. The breakage is straight in the circumferential direction and appear flat as if machined. The nearby area shows plastic deformation. It happens when the applied force exceeds the shear strength of the material. It happens when a high stiffness and strength gear is meshed with a gear which has a relatively low modulus of elasticity and weak material.
Applications of Gears in Various Industries
Robotics
Humanoid Robots
Semiconductor Equipment
Medical Device
Machine Tools
Industrial Automation
Food Processing Equipment
Related links :
齿轮的基本用语和尺寸计算
Free Gear Calculator
Calculation of Gear Dimensions


